AG


	AG: Mathematik in der HS MaHS/TIMSS

Leitung/ Team:	Rudi Kratschmer, Sieglinde Waasmaier, Reinhold Dürrschmidt, Christian Ehrenreich, Karl Peter Fuchs, Ulrich Lipp, Eduard Nalepa, Joachim Warmus, Heinrich Merz, Schulrat	Vertreter der Schulen in der "Fachschaft" Mahematik in der HS:
		HS Eichendorf: HS Niederviehbach: HS Reisbach: VS Moosthenning: VS Pilsting: VS Simbach: VS Wallersdorf:	Heinz Zimon Max Hofmeier Hans Graßl Andrea Weber Jutta Schätz Manfred Baier Heinrich Ertl

Fehler selbst suchen

Lasst die Schüler doch mal ihre Fehler selber suchen!
Kurzzusammenfassung: In einem Miniexperiment mussten Schüler als Verbesserung einer Mathematikprobearbeit ihre Fehler mit Hilfe einer Musterlösung selbst finden und die Arbeit selbst bewerten. Bei einer Wiederholung der Probe schnitten sie deutlich besser ab als eine Vergleichsgruppe, die die Probearbeit konventionell (Lehrer an der Tafel mit Musterlösung, Kinder schreiben im Heft mit) verbesserte.
Versuchsbeschreibung: In zwei 8. Hauptschulklassen wurde nach vergleichbarem Unterricht eine fast identische Geometrieprobe geschrieben (Siehe Beispielaufgabe Abb. 1). In der 8x sah die Verbesserung so aus: Die Schüler bekamen ihre unkorrigierte eigene Probearbeit (zur Sicherheit vor Unterschleif natürlich als Kopie) und eine Musterlösung mit Angabe der Punkte und Notenverteilung. Arbeitsauftrag: Korrigiere deine Probe selbst und gib dir auch selbst die Note nach dem Punkteschlüssel! Schau dir die Fehler genau an, damit du sie nicht nochmals machst! Wenn du Hilfe brauchst, dann frage deine Mitschüler in der Gruppe oder den Lehrer!

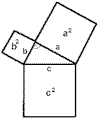
Abb 1: Eine Aufgabe aus der Probe	Abb 2: Die Musterlösung dazu
Die Schüler arbeiteten 45 Minuten selbständig. 11 der 22 Schüler kamen in dieser Zeit mit der Bitte um Hilfe zum Lehrer. Sie wurden nur dann im Einzelgespräch beraten, wenn sie auch gezielt fragten. Sonst wurden sie wieder weggeschickt. Dann wurde alles (Proben +Musterlösungen) wieder komplett eingesammelt (Damit entfiel ein Auswendiglernen.) und erst dann für den nächsten Tag die Wiederholung der Probe angekündigt. Die Kontrollgruppe, die Klasse 8y, verbesserte ihre Probe wie üblich. Der Lehrer teilte die korrigierten und benoteten Proben aus, schrieb die Musterlösungen an die Tafel und besprach sie im Klassenverband. Dann kündigte er ohne Zeitangabe eine Wiederholung der Probe an. Ergebnisse:
8x: selbständige Fehlersuche 8y: herkömmliche Verbesserung

Ein Vergleich der Veränderungen lässt vermuten, dass in der Klasse 8x zumindest im Kurzzeitgedächtnis mehr gespeichert wurde. Diskussion der Ergebnisse Die Aussagekraft dieses Experiments ist natürlich wegen der kleinen Stichprobe und der viele unkontrollierten Einflussvariablen nur eingeschränkt. Das bessere Ergebnis der 8x könnte neben dem Selbstkontrollverfahren auch durch andere Faktoren entstanden sein: Die Selbstkontrolle der 8x fand in der Stunde nach der ersten Probe statt, die zweite Probe gleich am nächsten Tag, in der 8y waren 1. Probe, Verbesserung und 2. Probe über eine Woche (mit Wochenende dazwischen) verstreut. Die Schüler der 8x wurden befragt und gaben mehrheitlich (14 von 22) an, sich in die Selbstkorrektur "ganz tief und voll konzentriert" oder "tief, aber nicht mit voller Kraft" "reingehängt zu haben. Keiner der 8 übrigen Schüler wollte ganz unkonzentriert gewesen sein. Vielleicht war die Klasse auch nur besonders konzentriert, weil der Lehrer meinte, es ginge "um ein Experiment". Die Frage, ob über die Speicherung im Kurzzeitgedächtnis auch etwas im Langzeitgedächtnis gelandet ist, wird eine erneute Wiederholung der Probe mit deutlichem zeitlichen Abstand zeigen. Trotz aller berechtigten Fragezeichen hinter den Ergebnissen, lässt das Experiment eine Folgerung für den Mathematikunterricht in der Hauptschuloberstufe zu: Schüler lernen auch dadurch, dass sie selbständig mit einer Lösungshilfe eigene Probearbeiten korrigieren.

Fragebogen zum Fach Mathematik
Wie beurteilst du das Fach Mathematik r mag ich sehr gern Begründe: ___________________________ r es geht so __________________________ r mag ich nicht __________________________ r mag ich gar nicht __________________________
Wie schätzt du deine Leistungen in Mathematik ein? Ich bin r ein guter Schüler r ich fasse den Lernstoff leicht auf r ich bin ein mittelmäßiger Schüler r ich verstehe nicht alles beim ersten Mal r ich bin ein schwacher Schüler r ich verstehe den Lernstoff nicht r ich mach die Hausaufgaben oft falsch oder kann sie nicht
Wie oft und wie lange lernst du für eine Matheprobe? r an einem Tag r an zwei Tagen r an _______________ r insgesamt ___________________Stunden
Eine Mathestunde gefällt mir, wenn ________________________________________________________ ________________________________________________________ _________________________________________________________
Eine Mathematikstunde gefällt mir nicht, wenn ________________________________________________________ ________________________________________________________ _________________________________________________________
Mathematik ist ein r sehr wichtiges r wichtiges r nicht wichtiges Fach
Welche Aufgaben magst du? (1 = sehr gern, 2 = gern, 3= es geht so, 4 = nicht so, 5 = gar nicht)
Kopfrechnen Textaufgaben Rechnen mit Zahlen (ohne Text) Geometrieaufgaben Aufgaben mit Tabellen und Schaubildern selbst gestellte Aufgaben Zahlenspiele Denkaufgaben	(____) (____) (____) (____) (____) (____) (____) (____)
Werden deine Fehler im Unterricht vom Lehrer berichtigt? r meistens r oft r selten r nie
Würdest du einmal je Woche freiwillig in eine AG Mathematik gehen (ohne Benotung) am Nachmittag? r ja r nein r manchmal
Ich arbeite am liebsten r alleine in Einzelarbeit r zusammen mit einem Partner r gemeinsam in einer Gruppe
Ich kann mich in Mathematik meistens r gut konzentrieren r wenig konzentrieren r fast gar nicht konzentrieren
Danke für deine ehrlichen Antworten!